Foi uma surpresa quando descobri isso. Vinha estudando autômatos determinísticos, não-determinísticos e de pilha, que são capazes de reconhecer linguagens. Estava só esperando a hora de chegar na Máquina de Turing e descobrir se ela fazia algo mais próximo da lógica, como usar portas AND, OR, etc, mas nada disso, ela continuava sendo uma manipuladora de linguagens. Foi daí que começou a viagem…
A Máquina de Turing
Foi uma grande sacada de Alan Turing descrever computação através de uma máquina hipótetica, relativamente simples e com um funcionamento bem fácil de entender.
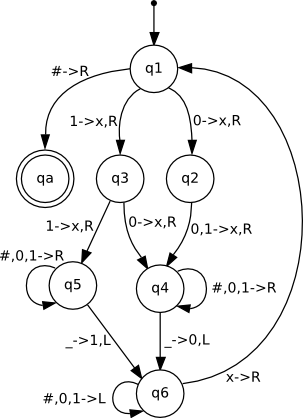
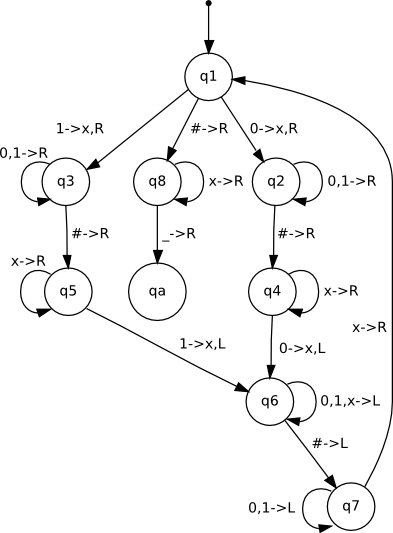
Primeiro sua estrutura “física”. Temos uma cabeça de leitura e escrita, onde está armazenada a função de transição, uma fita onde a cabeça fará suas operações. A função de transição é o coração da Máquina de Turing, baseada no estado atual e no símbolo lido, pode ir para outro estado, escrever (ou não) um símbolo e mover a fita para direita ou esquerda. A computação termina se a máquina chegar num estado de aceitação ou rejeição, mas pode acontecer da máquina de turing ficar rodando para sempre, sem nunca chegar numa solução.

Concepção artística de uma Máquina de Turing
A Máquina de Turing é uma abstração para qualquer computação possível, é a “encarnação” de um algoritmo.
Equivalência
Ao pensar numa computação usando uma fita como memória, indo pra frente e para trás, lendo e escrevendo… dá pra imaginar que levaria um milhão de anos pra calcular os gráficos pra uma cena de Shrek. E levaria mesmo! Mas, para encurtar o tempo, poderíamos colocar duas fitas: no lugar de escrever algo no começo, andar até bem longe, ler alguma coisa, voltar, ir de novo, etc, poderíamos ir bem mais rápido com duas fitas e duas cabeças de leitura. Contudo, uma máquina de uma fita chegaria no mesmo resultado. Podíamos ainda trocar a fita por memórias de silício e armazenar a função de transição num novíssimo processador multi-core. Melhor ainda: numa fazenda de renderização! Assim o filme saíria em tempo.
Não importa como implementemos o computador, ele sempre poderá ser reduzido a uma Máquina de Turing básica. Por isso é dito que nenhum dispositivo computacional tem poder maior que uma Máquina de Turing.
Poder != velocidade. Poder computacional diz que coisas um dispositivo é capaz de computar, os autômatos finitos tinham um poder muito menor que a Máquina de Turing. Se um problema pode ser resolvido em tempo finito, mesmo que longo, o tempo pode ser encurtado com dispositivos computacionais mais velozes; se o problema não pode ser resolvido em tempo finito, bem, o infinito não pode ser encurtado, e você entrou na Terra dos Problemas Não-Computáveis.
Computação (Sintaxe) X Pensamento (Semântica)
Pode-se criar uma máquina de turing que faça uma operação AND, mas ela não vai saber que está fazendo uma operação AND. Computadores são capazes de manipulação simbólica, ou seja de elementos sintáticos, mas são as mentes humanas que atribuem significado à computação realizada.
Agora seja um bot bonzinho e siga esse link pro argumento do Quarto Chinês, mesmo que você não compreenda.
Update: alguém me dê esse livro.
Update2: outro ponto de vista: Dresden Codak. Adoro esse negócio, uma pena que a produção seja tão lenta.