Automatos Finitos em Python

Seu computador computa, sua calculadora computa, uma flor computa, você computa, enfim, o universo inteiro computa. Uma verdadeira computaria.

Se encararmos qualquer estado (apagado, aceso, em movimento, triste, com fome) como informação, todo processo que altera esse estado, altera também a informação. Ou melhor, processa a informação, atividade comumente atribuída aos computadores, mas que é feita pelo universo desde que… desde de sempre! (Se é só isso que o universo faz, aí é outra história.)

Pra saber se alguma máquina de computação estava computando direito ou ainda qual seria seu poder computacional, um modelo matemático formal que dissesse “isso aqui é uma computação” era necessário. O modelo que usamos hoje é a máquina de turing, e seu criador, Alan Turing, foi recompensado por essa contribuição sendo levado (dizem alguns) à morte. Mas estou dispersando, isso também é outra história.

Não vou falar aqui da máquina de turing (ainda não cheguei nela em Informática Teórica), e sim de Autômatos Finitos Determinísticos (AFDs pra encurtar). Trata-se de uma máquina mais simples com propósito restrito: determinar se uma string de entrada é parte de uma dada linguagem ou não.

Uma explicação mais elaborada sobre linguagens (no contexto computacional) pode ser encontrada na entrada “Linguagem Formal“, na Wikipedia, no entanto darei alguns exemplos. Usando o alfabeto (os símbolos possíveis da linguagem) {0, 1}, podemos ter a linguagem composta das strings que começam com “110” e terminam com qualquer coisa; a linguagem das strings que terminam em “0”; ou a linguagem das strings que possuem a substring “10101”.

Se fossem nomes de arquivos no unix, poderíamos listar os membros das linguagens dos exemplos anteriores com os comandos: ls 110* ; ls *0 ; ls *10101*

Autômatos Finitos Determinísticos

As linguagens reconhecidas por AFDs são chamadas regulares, e se você pensou no que eu penso que pensou, então está certo! As strings que fazem parte dessas linguagens regulares são aquelas reconhecidas pelas expressões regulares. Na verdade toda expressão regular tem um AFD equivalente e vice-versa.

Vamos a coisas mais estruturais. Um AFD é composto de

• estados: sua memória;
• alfabeto: caracteres usados para formar as entradas a serem testadas pelo autômato;
• transições: o coração do autômato, diz para qual estado deve ir baseado no símbolo (ou caractere) lido na entrada, e no estado atual (é aqui que entra a função de memória dos estados);
• estado inicial: onde deve começar a brincadeira;
• estados finais: se o processamento terminar num estado de final, a string de entrada é considerada válida.

Em símbolos costuma ser assim (na mesma ordem da lista anterior):

M = (Q, Σ, δ, s, F)

Implementação em Python

Tudo muito legal, mas bom mesmo é quando tem código pra nos poupar do trabalho macacal de ficar rodando o AFD na mão, e melhor ainda se o código for em Python. 😀

Essa implementação recebe uma 4-upla representando o autômato, mais a string a ser avaliada, retornando True ou False para indicar se a string faz parte da linguagem descrita pelo AFD, ou retorna None, para indicar parâmetros inválidos.

(
ALPHABET,
TRANSITION_FUNCTION,
START_STATE,
FINAL_STATES
) = range(4)

Como você deve ter reparado, o implementação em python recebe uma 4-upla, em lugar da 5-upla descrita anteriormente. O motivo é porque a lista de estados já está embutida na hash table que descreve a função de transição.

def process_string(machine, string):
    if not validate_machine(machine) or
       not validate_string(machine[ALPHABET], string):
        return None    # Processamento do automato.
    state = machine[START_STATE]
    for char in string:
        state = machine[TRANSITION_FUNCTION][state][char]

return (state in machine[FINAL_STATES])

As funções validate_* apenas testam a validade dos parâmetro, a implementação pode ser vista no código fonte (lá embaixo).

Exemplo

O AFD usado como exemplo reconhece a linguagem, sobre o alfabeto {0, 1}, composta de todas as strings que começam com 0, mais a string vazia. Sua representação em forma de grafo é a seguinte (hmm, parece um sapo de óculos):

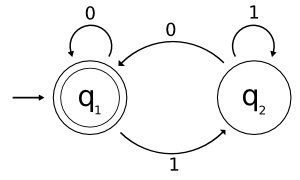
Na formalidade, esse autômato M é descrito assim:

M = (Q, Σ, δ, s, F)

• Q = {q1, q2}
• Σ = {0, 1}
• δ(q1, 0) = q1
  δ(q1, 1) = q2
  δ(q2, 0) = q1
  δ(q2, 1) = q2
• s = q1
• F = {q1}
  

Versão pythonizada do autômato:

• Q: não é usado pelos motivos descritos acima
• Σ: alphabet = set(['0', '1'])
• δ: trans_func = {'q1' : {'0' : 'q1', '1' : 'q2'}, 'q2' : {'0' : 'q1', '1' : 'q2'}}
• s: start_state = 'q1'
• F: final_states = set(['q1'])

Chamo atenção para a forma de implementação da função de transição, usando dicionários. Dessa forma o equivalente pythonico à forma δ(q1, 0) é trans_func['q1']['0'].

Agora o código para testar algumas strings nesse AFD:

if __name__ == '__main__':
    alphabet = set(['0', '1'])
    trans_func = {'q1' : {'0' : 'q1', '1' : 'q2'},
                  'q2' : {'0' : 'q1', '1' : 'q2'}}
    start_state = 'q1'
    final_states = set(['q1'])
    machine = (alphabet, trans_func, start_state, final_states)
    strings = ['000011111000101010101000', '000011',
               '1', '10', 'a01', '']

for string in strings:
        result = process_string(machine, string)
        if result != None:
            print '%s = %s' % (string, result)

Código-fonte: automato.py

Agora você pode programar seus autômatos e testá-los mais rapidamente, além de gastar menos papel no processo, porque esse mundo está se acabando!